Matrix calculations with Groovy™, Apache Commons Math, ojAlgo, Nd4j and EJML
Published: 2022-08-18 01:41PM
This blogs looks at performing matrix calculations with Groovy using various libraries: Apache Commons Math, ojAlgo, EJML, and Nd4j (part of Eclipse Deeplearning4j). We’ll also take a quick look at using the incubating Vector API for matrix calculations (JEPs 338, 414, 417, and 426).
Fibonacci
The Fibonacci sequence has origins in India centuries earlier but is named after the Italian author of the publication, The Book of Calculation, published in 1202. In that publication, Fibonacci proposed the sequence as a means to calculate the growth of idealized (biologically unrealistic) rabbit populations. He proposed that a newly born breeding pair of rabbits are put in a field; each breeding pair mates at the age of one month, and at the end of their second month they always produce another pair of rabbits; and rabbits never die, but continue breeding forever. Fibonacci posed the puzzle: how many pairs will there be in one year? The sequence goes like this:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233
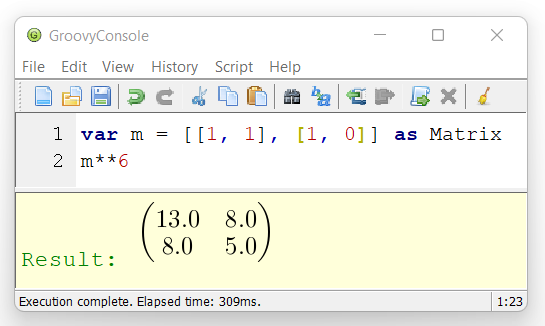
We can solve this problem using matrices. If we multiply the matrix ![]() by itself n times we get
by itself n times we get 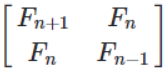 .
This is an operation known as matrix exponentiation.
Let’s explore this problem using four of the most popular
and maintained matrix libraries.
.
This is an operation known as matrix exponentiation.
Let’s explore this problem using four of the most popular
and maintained matrix libraries.
Apache Commons Math
Let’s explore solving this problem using Apache Commons Math. Apache Commons Math is a library of lightweight self-contained mathematics and statics components. Matrices are part of the linear algebra part of this library and for that context, matrices of double values are relevant. So, we’ll represent our Fibonacci numbers as double values.
double[][] data = [[1d, 1d], [1d, 0d]]
def m = MatrixUtils.createRealMatrix(data)
println m * m * m
println m**6Commons math has a factory method for creating matrixes from
double arrays. The names of the methods for multiplication and
exponentiation happen to align with Groovy’s methods available
for operator overloading, namely multiply and power,
so we can use Groovy’s convenient shorthands.
When we run the script, the output looks like this:
Array2DRowRealMatrix{{3.0,2.0},{2.0,1.0}}
Array2DRowRealMatrix{{13.0,8.0},{8.0,5.0}}
We could go a little further and print the values from the matrix, but the result is clear enough. We see the values in the Fibonacci sequence appearing in the output.
EJML
EJML (Efficient Java Matrix Library) is a linear algebra library for manipulating real, complex, dense, and sparse matrices. It is also a 100% Java solution. It has some novel features including import from Matlab and support for semirings (GraphBLAS) which can be used for graph algorithms where a sparse matrix may be used to represent a graph as an adjacency matrix or incidence matrix.
We can do the same calculation using EJML:
def m = new SimpleMatrix([[1d, 1d], [1d, 0d]] as double[][])
def ans = m.mult(m).mult(m)
println ans
6.times { ans = ans.mult(m) }
println ansThe name of the multiply method differs from the one where we can use automatic operator overloading shorthands, so we just call the method that EJML provides. See a little later under language extensibility on how we could in fact add support to use the same shorthands as we saw for Commons Math.
EJML doesn’t have an exponentiation method but we just call multiply the requisite number of times to achieve the same effect. Note that we bumped the number of iterations called for the second matrix, to reveal the next bunch of elements from the Fibonacci sequence.
Running this script has this output:
Type = DDRM , rows = 2 , cols = 2 3.0000E+00 2.0000E+00 2.0000E+00 1.0000E+00 Type = DDRM , rows = 2 , cols = 2 5.5000E+01 3.4000E+01 3.4000E+01 2.1000E+01
The first matrix has the same number as previously, and the second reveals the next numbers in the Fibonacci sequence (21, 34, and 55).
Nd4j
Nd4j provides functionality available on Python to Java users. It contains a mix of numpy operations and tensorflow/pytorch operations. Nd4l makes use of native backends to allow it to work on different platforms and provide efficient operation when scaling up.
The code for our Fibonacci solution is very similar to EJML:
def m = Nd4j.create([[1, 1], [1, 0]] as int[][])
def ans = m.mmul(m).mmul(m)
println ans
9.times { ans = ans.mmul(m) }
println ansOne feature that is different to the previous two libraries is that Nd4j supports integer matrices (as well as doubles and numerous other numerical and related types).
Running the script gives the following output:
...
[main] INFO org.nd4j.linalg.factory.Nd4jBackend - Loaded [CpuBackend] backend
...
[main] INFO org.nd4j.linalg.cpu.nativecpu.CpuNDArrayFactory - Binary level Generic x86 optimization level AVX/AVX2
[main] INFO org.nd4j.linalg.api.ops.executioner.DefaultOpExecutioner - Blas vendor: [OPENBLAS]
...
[[ 3, 2],
[ 2, 1]]
[[ 233, 144],
[ 144, 89]]
Again, the first matrix is the same as we have seen previously, the second has been bumped along the Fibonacci sequence by three more elements.
ojAlgo
The next library we’ll look at is ojAlgo (oj! Algorithms). It is an open source all-Java offering for mathematics, linear algebra and optimisation, supporting data science, machine learning and scientific computing. It claims to be the fastest pure-Java linear algebra library available and the project website provide links to numerous benchmarks backing that claim.
Here is the code for our Fibonacci example:
def factory = Primitive64Matrix.FACTORY
def m = factory.rows([[1d, 1d], [1d, 0d]] as double[][])
println m * m * m
println m**15We can see it supports the same operator overloading features we saw for Commons Math.
When we run the script, it has the following output:
org.ojalgo.matrix.Primitive64Matrix < 2 x 2 >
{ { 3.0, 2.0 },
{ 2.0, 1.0 } }
org.ojalgo.matrix.Primitive64Matrix < 2 x 2 >
{ { 987.0, 610.0 },
{ 610.0, 377.0 } }
As expected, the first matrix is as we’ve seen before, while the second reveals the next three numbers in the sequence.
Exploring the Vector API and EJML
From JDK16, various versions (JEPs 338, 414, 417, 426) of the Vector API have been available as an incubating preview feature. The HotSpot compiler has previously already had some minimal optimisations that can leverage vector hardware instructions but the Vector API expands the scope of possible optimisations considerably. We could look at writing our own code that might make use of the Vector API and perhaps perform our matrix multiplications ourselves. But, one of the libraries has already done just that, so we’ll explore that path.
The main contributor to the EJML library has published a
repo
for the purposes of very early prototyping and benchmarking.
We’ll use the methods from one of its classes to explore use
of the vector API for our Fibonacci example. The
MatrixMultiplication class has three methods:
mult_ikj_simple is coded in the way any of us might write a
multiplication method as a first pass from its definition without
any attempts at optimisation, mult_ikj is coded in a
highly-optimised fashion and corresponds to the code EJML would
normally use, and mult_ikj_vector uses the Vector API. Note, you can think of these methods as "one layer down" from the mult
method we called in the previous example, i.e. the mult method
we used previously would be calling one of these under the covers.
That’s why we pass the internal "matrix" representation instead
of our SimpleMatrix instance.
For our little calculations, the optimisations offered by the
Vector API would not be expected to be huge. However, we’ll do
our calculation for generating the matrix we did as a first step
for all of the libraries and we’ll do it in a loop with 1000
iterations for each of the three methods (mult_ikj_simple,
mult_ikj, and mult_ikj_vector). The code looks like this:
def m = new SimpleMatrix([[1, 1], [1, 0]] as double[][])
double[] expected = [3, 2, 2, 1]
def step1, result
long t0 = System.nanoTime()
1000.times {
step1 = new SimpleMatrix(2, 2)
result = new SimpleMatrix(2, 2)
MatrixMultiplication.mult_ikj_simple(m.matrix, m.matrix, step1.matrix)
MatrixMultiplication.mult_ikj_simple(step1.matrix, m.matrix, result.matrix)
assert result.matrix.data == expected
}
long t1 = System.nanoTime()
1000.times {
step1 = new SimpleMatrix(2, 2)
result = new SimpleMatrix(2, 2)
MatrixMultiplication.mult_ikj(m.matrix, m.matrix, step1.matrix)
MatrixMultiplication.mult_ikj(step1.matrix, m.matrix, result.matrix)
assert result.matrix.data == expected
}
long t2 = System.nanoTime()
1000.times {
step1 = new SimpleMatrix(2, 2)
result = new SimpleMatrix(2, 2)
MatrixMultiplication.mult_ikj_vector(m.matrix, m.matrix, step1.matrix)
MatrixMultiplication.mult_ikj_vector(step1.matrix, m.matrix, result.matrix)
assert result.matrix.data == expected
}
long t3 = System.nanoTime()
printf "Simple: %6.2f ms\n", (t1 - t0)/1000_000
printf "Optimized: %6.2f ms\n", (t2 - t1)/1000_000
printf "Vector: %6.2f ms\n", (t3 - t2)/1000_000This example was run on JDK16 with the following VM options:
–enable-preview –add-modules jdk.incubator.vector.
The output looks like this:
WARNING: Using incubator modules: jdk.incubator.vector
Simple: 116.34 ms
Optimized: 34.91 ms
Vector: 21.94 ms
We can see here that we have some improvement even for our trivial little calculation. Certainly, for biggest problems, the benefit of using the Vector API could be quite substantial.
We should give a big disclaimer here. This little microbenchmark using a loop of 1000 will give highly variable results and was just done to give a very simple performance comparison. For a more predictable comparison, consider running the jmh benchmark in the aforementioned repo. And you may wish to wait until the Vector API is out of preview before relying on it for any production code - but by all means, consider trying it out now.
Leslie Matrices
Earlier, we described the Fibonacci sequence as being for unrealistic rabbit populations, where rabbits never died and continued breeding forever. It turns out that Fibonacci matrices are a special case of a more generalised model which can model realistic rabbit populations (among other things). These are Leslie matrices. For Leslie matrices, populations are divided into classes, and we keep track of birth rates and survival rates over a particular period for each class. We store this information in a matrix in a special form. The populations for each class for the next period can be calculated from those for the current period through multiplication by the Leslie matrix.
This technique can be used for animal populations or human population calculations. A Leslie matrix can help you find out if there will be enough GenX, Millenials, and GenZ tax payers to support an aging and soon retiring baby boomer population. Sophisticated animal models might track populations for an animal and for its predators or its prey. The survival and birth rates might be adjusted based on such information. Given that only females give birth, Leslie models will often be done only in terms of the female population, with the total population extrapolated from that.
We’ll show an example for kangaroo population based on this video tutorial for Leslie matrices. It can help us find out if the kangaroo population is under threat (perhaps drought, fires or floods have impacted their feeding habitat) or if favorable conditions are leading to overpopulation.
Following that example, we divide kangaroos into 3 population classes: ages 0 to 3, 3 to 6, and 6 to 9. We are going to look at the population every three years. The 0-3 year olds birthrate (B1) is 0 since they are pre-fertile. The most fertile 3-6 year olds birthrate (B2) is 2.3. The old roos (6-9) have a birthrate (B3) of 0.4. We assume no kangaroos survive past 9 years old. 60% (S1) of the young kangaroos survive to move into the next age group. 30% (S2) of the middle-aged kangaroos survive into old age. Initially, we have 400 kangaroos in each age group.
Here is what the code looks like for this model:
double[] init = [400, // 0..<3
400, // 3..<6
400] // 6..9
def p0 = MatrixUtils.createRealVector(init)
println "Initial populations: $p0"
double[][] data = [
[0 , 2.3, 0.4], // B1 B2 B3
[0.6, 0, 0 ], // S1 0 0
[0 , 0.3, 0 ] // 0 S2 0
]
def L = MatrixUtils.createRealMatrix(data)
def p1 = L.operate(p0)
println "Population after 1 round: $p1"
def p2 = L.operate(p1)
println "Population after 2 rounds: $p2"
def L10 = L ** 10
println "Population after 10 rounds: ${L10.operate(p0).toArray()*.round()}"This code produces the following output:
Initial populations: {400; 400; 400}
Population after 1 round: {1,080; 240; 120}
Population after 2 rounds: {600; 648; 72}
Population after 10 rounds: [3019, 2558, 365]
After the first round, we see many young roos but a worrying drop off in the older age groups. After the second round, only the oldest age group looks worryingly small. However, with the healthy numbers in the young generation, we can see that after 10 generations that indeed, the overall population is not at risk. In fact, overpopulation might become a problem.
Encryption with matrices
An early technique to encrypt a message was the Caesar cipher. It substitutes letters in the alphabet by the letter shifted a certain amount along in the alphabet, e.g. "IBM" becomes "HAL" if shifting to the previous letter and "VMS" becomes "WNT" if shifting one letter forward in the alphabet. This kind of cipher can be broken by looking at frequency analysis of letters or pattern words.
The Hill cipher improves upon the Caesar cipher by factoring multiple letters into each letter of the encrypted text. Using matrices made it practical to look at three or more symbols at once. In general, an N-by-N matrix (the key) is multiplied by an encoding of the message in matrix form. The result is a matrix representation (encoded form) of the encrypted text. We use the inverse matrix of our key to decrypt or message.
We need to have a way to convert our text message to and from
a matrix. A common scheme is to encode A as 1, B as 2, and so on.
We’ll just use the ascii value for each character. We define
encode and decode methods to do this:
double[][] encode(String s) { s.bytes*.intValue().collate(3) as double[][] }
String decode(double[] data) { data*.round() as char[] }We’ll define a 2-by-2 matrix as our key and use it to encrypt. We’ll find the inverse of our key and use that to decrypt. If we wanted to, we could use a 3-by-3 key for improved security at the cost of more processing time.
Our code looks like this:
def message = 'GROOVY'
def m = new SimpleMatrix(encode(message))
println "Original: $message"
def enKey = new SimpleMatrix([[1, 3], [-1, 2]] as double[][])
def encrypted = enKey.mult(m)
println "Encrypted: ${decode(encrypted.matrix.data)}"
def deKey = enKey.invert()
def decrypted = deKey.mult(encrypted)
println "Decrypted: ${decode(decrypted.matrix.data)}"When run, it has the following output:
Original: GROOVY Encrypted: ĴŔŚWZc Decrypted: GROOVY
This offers far more security than the Caesar cipher, however, given today’s computing availability, Hill ciphers can still eventually be broken with sufficient brute force. For this reason, Hill ciphers are seldom used on their own for encryption, but they are often used in combination with other techniques to add diffusion - strengthening the security offered by the other techniques.
Shape manipulation
Our final example looks at geometrically transforming shapes. To do this, we represent the points of the shape as vectors and multiply them using transforms represented as matrices. We need only worry about the corners, since we’ll use Swing to draw our shape, and it has a method for drawing a polygon by giving its corners.
First we’ll use Groovy’s SwingBuilder to set up our frame:
new SwingBuilder().edt {
def frame = frame(title: 'Shapes', size: [420, 440], show: true, defaultCloseOperation: DISPOSE_ON_CLOSE) {
//contentPane.background = Color.WHITE
widget(new CustomPaintComponent())
}
frame.contentPane.background = Color.WHITE
}We aren’t really use much of SwingBuilder’s functionality here but if we wanted to add more functionality, SwingBuilder would make that task easier.
We will actually draw our shapes within a custom component.
We’ll define a few color constants, a drawPolygon method which
given a matrix of points will draw those points as a polygon.
We’ll also define a vectors method to convert a list of points
(the corners) into vectors, and a transform method which is a
factory method for creating a transform matrix.
Here is the code:
class CustomPaintComponent extends Component {
static final Color violet = new Color(0x67, 0x27, 0x7A, 127)
static final Color seaGreen = new Color(0x69, 0xCC, 0x67, 127)
static final Color crystalBlue = new Color(0x06, 0x4B, 0x93, 127)
static drawPolygon(Graphics g, List pts, boolean fill) {
def poly = new Polygon().tap {
pts.each {
addPoint(*it.toRawCopy1D()*.round()*.intValue().collect { it + 200 })
}
}
fill ? g.fillPolygon(poly) : g.drawPolygon(poly)
}
static List<Primitive64Matrix> vectors(List<Integer>... pts) {
pts.collect{ factory.column(*it) }
}
static transform(List<Number>... lists) {
factory.rows(lists as double[][])
}
void paint(Graphics g) {
g.drawLine(0, 200, 400, 200)
g.drawLine(200, 0, 200, 400)
g.stroke = new BasicStroke(2)
def triangle = vectors([-85, -150], [-145, -30], [-25, -30])
g.color = seaGreen
drawPolygon(g, triangle, true)
// transform triangle
...
def rectangle = vectors([0, -110], [0, -45], [95, -45], [95, -110])
g.color = crystalBlue
drawPolygon(g, rectangle, true)
// transform rectangle
...
def trapezoid = vectors([50, 50], [70, 100], [100, 100], [120, 50])
g.color = violet
drawPolygon(g, trapezoid, true)
// transform trapezoid
...
}
}When we run this code we see our three shapes:
We can now add our transforms. We’ll have one which rotate by 90 degrees anti-clockwise. Another which enlarges a shape by 25% and one that shrinks a shape by 25%. We can combine transforms simply by multiplying them together. We’ll make two transformations of our triangle. We’ll rotate in both cases but we’ll shrink one and enlarge the other. We apply the transform simply by multiplying each point by the transform matrix. Then we’ll draw both transformed shapes as an outline rather than filled (to make it easier to distinguish the original and transformed versions). Here is the code:
def rot90 = transform([0, 1], [-1, 0])
def bigger = transform([1.25, 0], [0, 1.25])
def smaller = transform([0.75, 0], [0, 0.75])
def triangle_ = triangle.collect{ rot90 * bigger * it }
drawPolygon(g, triangle_, false)
triangle_ = triangle.collect{ rot90 * smaller * it }
drawPolygon(g, triangle_, false)For our rectangle, we’ll have one simple transform which flips the shape in the vertical axis. A second transform combines multiple changes in one transform. We could have split this into smaller transforms and the multiplied them together - but here they are all in one. We flip in the horizontal access and then apply a shear. We then draw the transformed shapes as outlines:
def flipV = transform([1, 0], [0, -1])
def rectangle_ = rectangle.collect{ flipV * it }
drawPolygon(g, rectangle_, false)
def flipH_shear = transform([-1, 0.5], [0, 1])
rectangle_ = rectangle.collect{ flipH_shear * it }
drawPolygon(g, rectangle_, false)For our trapezoid, we create a transform which rotates 45 degrees anti-clockwise (recall sin 45° = cos 45° = 0.707). Then we create 6 transforms rotating at 45, 90, 135 and so forth. We draw each transformed shape as an outline:
def rot45 = transform([0.707, 0.707], [-0.707, 0.707])
def trapezoid_
(1..6).each { z ->
trapezoid_ = trapezoid.collect{ rot45 ** z * it }
drawPolygon(g, trapezoid_, false)
}When we run the entire example, here is what the output looks like:
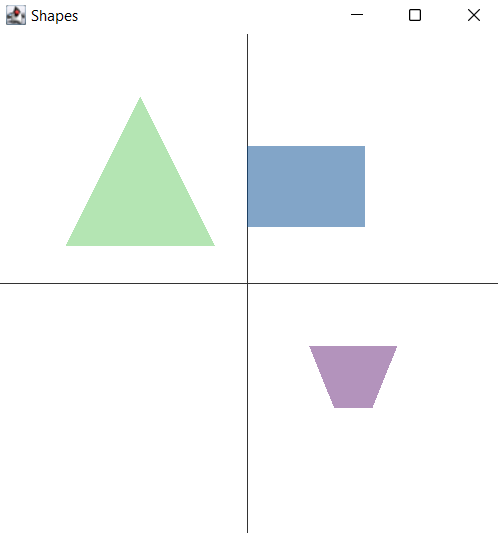
We can see here that matrix transforms give us powerful ways to manipulate images. We have used 2D images here, but the same techniques would apply to 3D shapes.
Language and tool extensibility
We saw earlier that some of the examples could make use of Groovy operator shorthand syntax, while others couldn’t. Here is a summary of some common methods in the libraries:
Groovy operator |
+ |
- |
* |
** |
Groovy method |
plus |
minus |
multiply |
power |
Commons math |
|
|
|
|
EJML |
|
|
|
- |
Nd4j |
|
|
|
- |
ojAlgo |
|
|
|
|
Where the library used the same name as Groovy’s method, the shorthand could be used.
Groovy offers numerous extensibility features. We won’t go into all of the details but instead refer readers to the History of Groovy paper which gives more details.
In summary, that paper defined the following extensions for Commons Math matrices:
RealMatrix.metaClass {
plus << { RealMatrix ma -> delegate.add(ma) }
plus << { double d -> delegate.scalarAdd(d) }
multiply { double d -> delegate.scalarMultiply(d) }
bitwiseNegate { -> new LUDecomposition(delegate).solver.inverse }
constructor = { List l -> MatrixUtils.createRealMatrix(l as double[][]) }
}This fixes some of the method name discrepancies in the above
table. We can now use the operator shorthand for matrix and
scalar addition as well as scalar multiply. We can also use
the ~ (bitwiseNegate) operator when finding the inverse.
The mention of double[][] during matrix construction is
now also gone.
The paper goes on to discuss how to automatically add the necessary imports for a matrix library and provide aliases if needed. The imports aren’t shown for the code listings in this blog but are in the listings in the sample code repo. In any case, the imports can be "configured away" as the paper discusses. The end result is our code in its entirety can look like this:
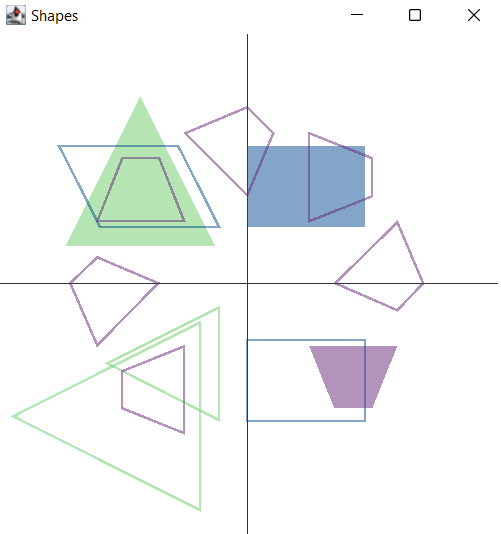
var m = [[1, 1], [1, 0]] as Matrix
m**6The paper also discusses tooling extensibility, in particular the
visualisation aspects of the GroovyConsole. It shows how to define
an output transform which renders any matrix result using a
jlatexmath library. So instead of seeing
Array2DRowRealMatrix{{13.0,8.0},{8.0,5.0}}, they will see
a graphical rendition of the matrix. So, the final end-user
experience when using the GroovyConsole looks like this:
When using in Jupyter style environments, other pretty output styles may be supported.
Further information
-
Apache Commons Math User Guide and GitHub mirror
-
ojAlgo website and GitHub repo
-
EJML website and GitHub repo
-
Nd4j documentation and GitHub repo
-
Leslie Matrices for population age distribution modelling video
Conclusion
We have examined a number of simple applications of matrices using the Groovy programming language and the Apache Commons Math, ojAlgo, Nd4j, and EJML libraries. You should be convinced that using matrices on the JVM isn’t hard, and you have numerous options. We also saw a brief glimpse at the Vector API which looks like an exciting addition to the JVM (hopefully arriving soon in non-preview mode).
