Solving cryptarithmetic puzzles with Groovy™ and constraint programming using Choco, JaCoP, and OR-Tools
Published: 2022-09-05 01:43PM
Introduction
When writing solutions to problems, we frequently strive to hide away implementation details. In Object-oriented (OO) programming, we might build a rich hierarchy of classes with carefully thought-out methods so that our final solution can be expressed in terms of simple nouns and verbs (methods and class instances) in our domain model. When applying functional programming idioms, we will strive to emphasise the relationship between inputs and outputs and hide away side effects and iterative steps.
Constraint programming (within the same family as logic programming) also strives to hide away details. Instead of expressing an iterative implementation, it focuses on expressing declarative properties of a solution. A solver is responsible for working out the exact implementation steps.
When using constraint programming, we develop a model consisting of variables, the domain of values each variable may hold, and additional constraints between the variables. A solver does all the work. It may employ heuristic searching, inference, propagation, symmetry and backtracking to find possible solutions. We may be able to (or want to, or need to) guide the solver as to which techniques and strategies it should use. Constraint programming has been used to solve various kinds of problems including scheduling problems, and excels at problems with combinatorial possibilities that are too irregular for other mathematical optimisations. Frequently used illustrative problems are Sudoku and Wordle solvers, N-Queen problems, and other kinds of puzzles. We’ll just look at cryptarithmetic puzzles.
Cryptarithmetic Problems
Cryptarithmetic problems (also known as alphametics, verbal arithmetic, cryptarithm, and word addition) are a type of mathematical game where a mathematical equation is presented where digits in the equation are replaced by letters. Traditionally, each letter usually represents a unique number, and numbers don’t start with the digit zero. If we look at one sample problem:
T |
O |
||
+ |
G |
O |
|
= |
O |
U |
T |
We can reason about what the solution can be by hand:
-
T, O, U, and G must be all different (game rule)
-
T, G, and O will be between 1 and 9, and U is between 0 and 9 (game rule)
-
If we added the two biggest 2-digit numbers, (99 + 99) we’d get 198, so O must be 1
-
Looking at the right-most "units" column, 1 + 1 equals 2, so T must be 2
-
Looking at the "tens" column, we know there is a carry of 1 (since O is 1), and we know T is 2, so G must be 8 or 9. If G was 9, U would be 1, but it can’t be the same as O, so G must be 8 and U must be 0.
When solving by hand, we typically reason about individual columns and account for the "carry"to the next column. We’ll come back to this point later but first, let’s look at a slightly bigger problem:
S |
E |
N |
D |
||
+ |
M |
O |
R |
E |
|
= |
M |
O |
N |
E |
Y |
Solving with Brute Force
This problem isn’t huge, so we can solve with brute force. We simply try all possible values for the letters in the puzzle:
for (s in 1..9)
for (e in 0..9)
for (n in 0..9)
for (d in 0..9)
for (m in 1..9)
for (o in 0..9)
for (r in 0..9)
for (y in 0..9)
if ([s, e, n, d, m, o, r, y].toSet().size() == 8) {
def send = 1000 * s + 100 * e + 10 * n + d
def more = 1000 * m + 100 * o + 10 * r + e
def money = 10000 * m + 1000 * o + 100 * n + 10 * e + y
if (send + more == money) {
println "s = $s, e = $e, n = $n, d = $d"
println "m = $m, o = $o, r = $r, y = $y"
}
}This isn’t very efficient though. It calculates 81 million combinations for the variables before skipping all but 1.5 million of them (since most won’t be unique). All up it might execute in the low tens of seconds.
Alternatively, Groovy supports calculating permutations, so we can simplify our solution to a single for loop (with some tests to eliminate unhelpful iterations):
def digits = 0..9
for (p in digits.permutations()) {
if (p[-1] < p[-2]) continue
def (s, e, n, d, m, o, r, y) = p
if (s == 0 || m == 0) continue
def send = 1000 * s + 100 * e + 10 * n + d
def more = 1000 * m + 100 * o + 10 * r + e
def money = 10000 * m + 1000 * o + 100 * n + 10 * e + y
if (send + more == money) {
println "s = $s, e = $e, n = $n, d = $d"
println "m = $m, o = $o, r = $r, y = $y"
}
}This has the advantage of only generating unique combinations. It will execute in seconds.
Running either of these solutions yields:
s = 9, e = 5, n = 6, d = 7 m = 1, o = 0, r = 8, y = 2
Using Constraint Programming
For the brute force approaches, we had a condition which checked any potential candidate answer to see if it was a correct solution. We had to be very explicit in how we wanted the potential candidates to be created. For constraint programming, we instead define variables to represent the problem, any known bounds on those variables, and we specify any other known properties of the solution, which in our case will be something similar to the condition we had to check if the answer was correct previously. Let’s examine how to do that with three libraries, one with a variation.
Choco
Here is the code using the Choco library:
new Model("SEND+MORE=MONEY").with {
def (S, M) = ['S', 'M'].collect { intVar(it, 1, 9) }
def (E, N, D, O, R, Y) = ['E', 'N', 'D', 'O', 'R', 'Y'].collect { intVar(it, 0, 9) }
allDifferent(S, E, N, D, M, O, R, Y).post()
IntVar[] ALL = [
S, E, N, D,
M, O, R, E,
M, O, N, E, Y ]
int[] COEFFS = [
1000, 100, 10, 1,
1000, 100, 10, 1,
-10000, -1000, -100, -10, -1 ]
scalar(ALL, COEFFS, "=", 0).post()
println solver.findSolution()
}We define our variables and their bounds (domain).
We use an allDifferent global constraint to specify the
uniqueness requirement and a scalar constraint that
ensures that our variables multiplied by their respective
scalar coefficients equal 0. This lets us factor in whether
the particular variable is representing the "units" column,
the "10s" column, the "100s" column etc. This captures the
"puzzle addition" constraint. We then ask the solver to find
the solution. We could just as easily have asked for all
solutions (if more than one existed).
This is typical of how we solve such problems. We either define constraints directly between one or more variables or use whatever global constraints our library might support. If our library doesn’t support the constraint we need, we find a way to express it using multiple simpler constraints.
The end result is that our code is more declarative than our brute force approaches, and the solution is found in tens of milliseconds. The solver has very efficient strategies for solving such puzzles.
JaCoP
We can solve the same problem using JaCoP:
def store = new Store()
def (S, M) = ['S', 'M'].collect { new IntVar(store, it, 1, 9) }
def (E, N, D, O, R, Y) = ['E', 'N', 'D', 'O', 'R', 'Y'].collect { new IntVar(store, it, 0, 9) }
var ctr = new Alldifferent(S, E, N, D, M, O, R, Y)
store.impose(ctr)
IntVar[] ALL = [
S, E, N, D,
M, O, R, E,
M, O, N, E, Y ]
int[] COEFFS = [
1000, 100, 10, 1,
1000, 100, 10, 1,
-10000, -1000, -100, -10, -1 ]
var lin = new LinearInt(ALL, COEFFS, "==", 0)
store.impose(lin)
var label = new DepthFirstSearch()
var select = new InputOrderSelect(store, ALL, new IndomainMin())
label.labeling(store, select)There are some slight differences in this API, but nearly everything has a one-to-one correspondence to what we saw earlier. We are explicitly selecting search strategies and selection strategies here whereas with Choco, defaults were chosen for us. In both cases, explicit creation of such classes allows the strategies to be altered for particular scenarios if needed.
When run, the output looks like this:
Labeling has finished with return value of true DFS1: DFS([S = 9, E = 5, N = 6, D = 7, M = 1, O = 0, R = 8, Y = 2], InputOrder, (org.jacop.search.IndomainMin@45394b31))
We can see here the code is very similar as is the execution time.
OR-Tools
We can repeat the solution using OR-Tools. Here is the code:
Loader.loadNativeLibraries()
new Solver('Send+More=Money').with {
def s = makeIntVar(1, 9, 's')
def e = makeIntVar(0, 9, 'e')
def n = makeIntVar(0, 9, 'n')
def d = makeIntVar(0, 9, 'd')
def m = makeIntVar(1, 9, 'm')
def o = makeIntVar(0, 9, 'o')
def r = makeIntVar(0, 9, 'r')
def y = makeIntVar(0, 9, 'y')
IntVar[] all = [s, e, n, d, m, o, r, y]
IntVar[] scalar = [s, e, n, d, m, o, r, e, m, o, n, e, y]
int[] coeffs = [
1000, 100, 10, 1, // S E N D +
1000, 100, 10, 1, // M O R E =
-10000, -1000, -100, -10, -1 // M O N E Y
]
addConstraint(makeScalProdEquality(scalar, coeffs, 0))
addConstraint(makeAllDifferent(all))
def db = makePhase(all, INT_VAR_DEFAULT, INT_VALUE_DEFAULT)
newSearch(db)
while (nextSolution()) {
println all.join(' ')
}
endSearch()
// Statistics
println "Solutions: ${solutions()}"
println "Failures: ${failures()}"
println "Branches: ${branches()}"
println "Wall time: ${wallTime()}ms"
}It has this output when run:
s(9) e(5) n(6) d(7) m(1) o(0) r(8) y(2) Solutions: 1 Failures: 5 Branches: 10 Wall time: 60ms
OR-Tools is written in C++ but has interfaces for numerous languages including Java - which is perfect for Groovy use.
Choco with JSR331
It is great to have multiple libraries to pick from but having a standard API can help switching between such libraries. This is where JSR331 comes in. It defines a standard API for interacting with constraint solvers and linear solves. Here we use a JSR331 implementation backed by an earlier version of the Choco library. The code looks like this:
import javax.constraints.*
ProblemFactory.newProblem('SEND+MORE=MONEY').with {
def (S, M) = ['S', 'M'].collect { variable(it, 1, 9) }
def (E, N, D, O, R, Y) = ['E', 'N', 'D', 'O', 'R', 'Y'].collect { variable(it, 0, 9) }
postAllDifferent(S, E, N, D, M, O, R, Y)
Var[] ALL = [
S, E, N, D,
M, O, R, E,
M, O, N, E, Y]
int[] COEFFS = [
1000, 100, 10, 1,
1000, 100, 10, 1,
-10000, -1000, -100, -10, -1]
post(COEFFS, ALL, '=', 0)
def solver = getSolver()
def solution = solver.findSolution()
println solution ?: 'No solution'
solver.logStats()
}It is quite similar to earlier examples but now exclusively uses the JSR331 classes in the javax.constraint package. There are implementations of those classes backed by several implementations. So, indeed it would be possible to swap between them. When run, the output is:
Solution #1: S[9] M[1] E[5] N[6] D[7] O[0] R[8] Y[2]
Having said that, at the time of writing, JSR331 popularity doesn’t appear to be on the rise. Most folks using constraint programming libraries seem to be using the direct library classes. Indeed, the version of the Choco implementation used by the JSR331 implementation is over 10 years old.
Incorporating Carry
The scalar product global constraint we have used in the previous examples is very powerful and probably would be our first choice for this problem. We can, however, model constraint programming problems in multiple ways, so let’s look at a solution that avoids that global constraint.
Instead, we will develop a model that mirrors how we reasoned
about the original TO + GO = OUT problem that we
solved by hand. For that, we just considered a column at a time
and accounted for the carry. We’ll explicitly introduce variables
to hold the carry (0 if no carry, or 1 if there is a carry) into
our model. Then we’ll express the mathematical constraints that
are applicable for each column.
Here is the code:
new Model("SEND+MORE=MONEY").with {
def (S, M) = ['S', 'M'].collect { intVar(it, 1, 9) }
def (E, N, D, O, R, Y) = ['E', 'N', 'D', 'O', 'R', 'Y'].collect { intVar(it, 0, 9) }
def C = (0..3).collect{ intVar("C$it", 0, 9) }
allDifferent(S, E, N, D, M, O, R, Y).post()
C[3] .eq(M).post() // C3 C2 C1 C0
C[2].add(S).add(M).eq(O.add(C[3].mul(10))).post() // S E N D
C[1].add(E).add(O).eq(N.add(C[2].mul(10))).post() // M O R E
C[0].add(N).add(R).eq(E.add(C[1].mul(10))).post() // -------------
D .add(E).eq(Y.add(C[0].mul(10))).post() // M O N E Y
println solver.findSolution()
}We can see that there is now no scalar product global constraint any more but instead the constraints for each column.
When run, the output looks like this:
Solution: S=9, M=1, E=5, N=6, D=7, O=0, R=8, Y=2, C0=1, C1=1, C2=0, C3=1, sum_exp_1=9, sum_exp_2=10, (C3*10)=10, sum_exp_3=10, sum_exp_4=6, sum_exp_5=6, (C2*10)=0, sum_exp_6=6, sum_exp_7=7, sum_exp_8=15, (C1*10)=10, sum_exp_9=15, sum_exp_10=12, (C0*10)=10, sum_exp_11=12,
We can see that as we were defining our constraints for each column, subexpressions were being created in the model which are reflected in the solution. They are if you like, temporary calculations along the way to getting the answer - or more accurately a snapshot of ever-changing temporary calculations. They don’t form part of the answer that interests us, so we would be free to just print out the part of the solution which interests us if we wanted.
Creating a DSL
The previous example has lots of calls to add and mul methods.
We can create a little bit of a DSL to provide some syntactic
sugar to our previous examples to allow use of Groovy’s operator
overloading, support ranges when specifying the domain of a
variable, and a few other niceties. Our code becomes:
model("SEND+MORE=MONEY") {
def (S, M) = ['S', 'M'].collect { intVar(it, 1..9) }
def (E, N, D, O, R, Y) = ['E', 'N', 'D', 'O', 'R', 'Y'].collect { intVar(it, 0..9) }
def C = intVarArray(4, 0..1)
[allDifferent(S, E, N, D, M, O, R, Y), // C3 C2 C1 C0
C[3] .eq(M), // S E N D
(C[2] + S + M).eq(O + C[3] * 10), // M O R E
(C[1] + E + O).eq(N + C[2] * 10), // -------------
(C[0] + N + R).eq(E + C[1] * 10), // M O N E Y
(D + E).eq(Y + C[0] * 10)]*.post()
println solver.findSolution()
}It has the same output as previously.
You might wonder how the solver finds the solution. You can watch the variables in the debugger and use tools like choco-cpviz but it is a quite convoluted process until you are used to it. We’ll try to give you a flavor of what is going on here. Basically, there will be various steps of pruning wherever possible and branching with possible backtracking. Below are some snapshots for our example above.
To start with, we have nearly 90 light green squares which represents our problem search space. We walk our way through the rules looking for ways to prune the search space:

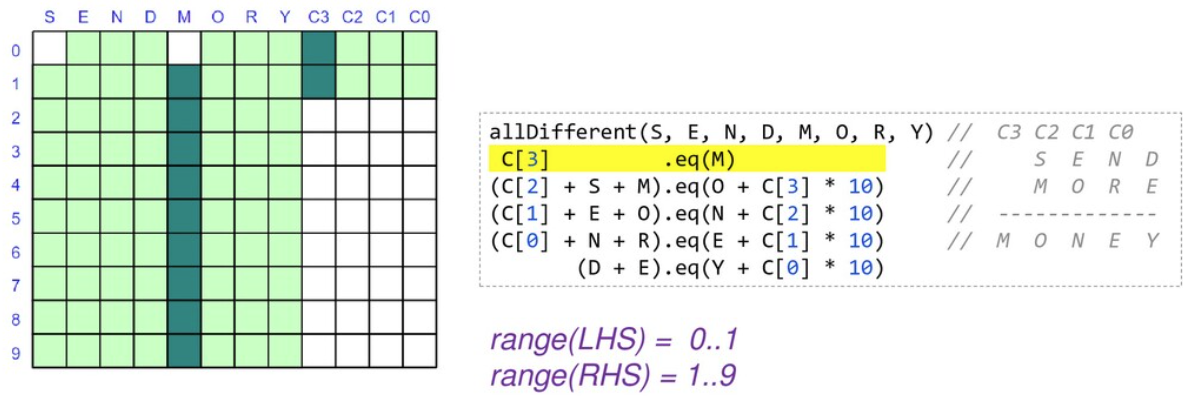


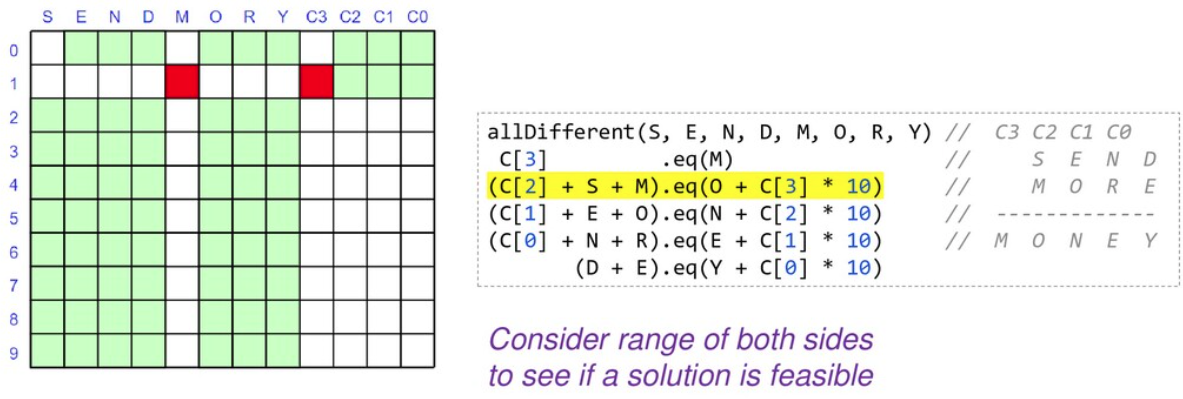
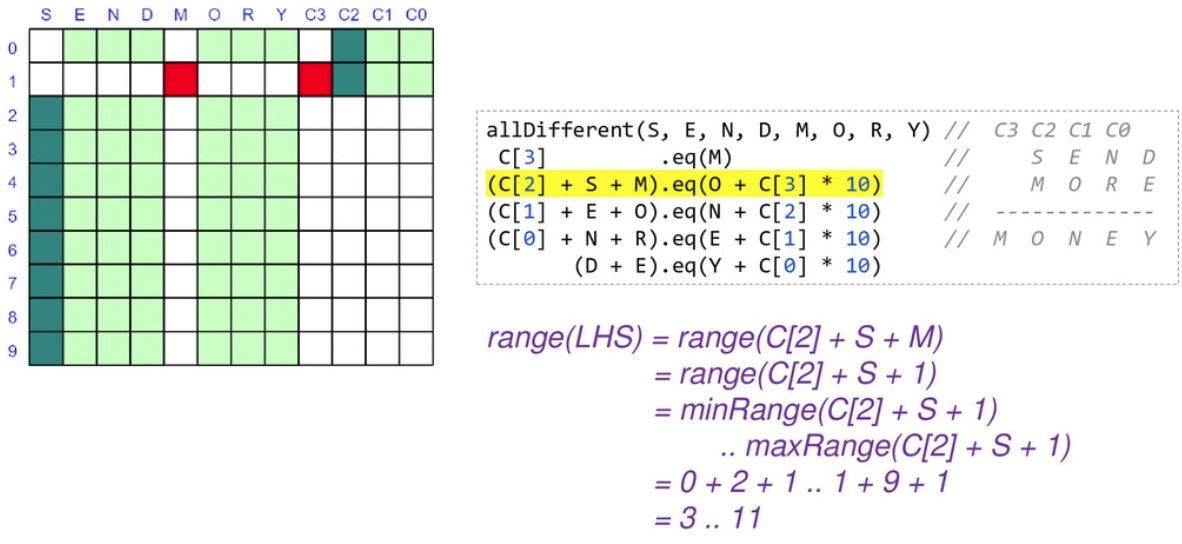



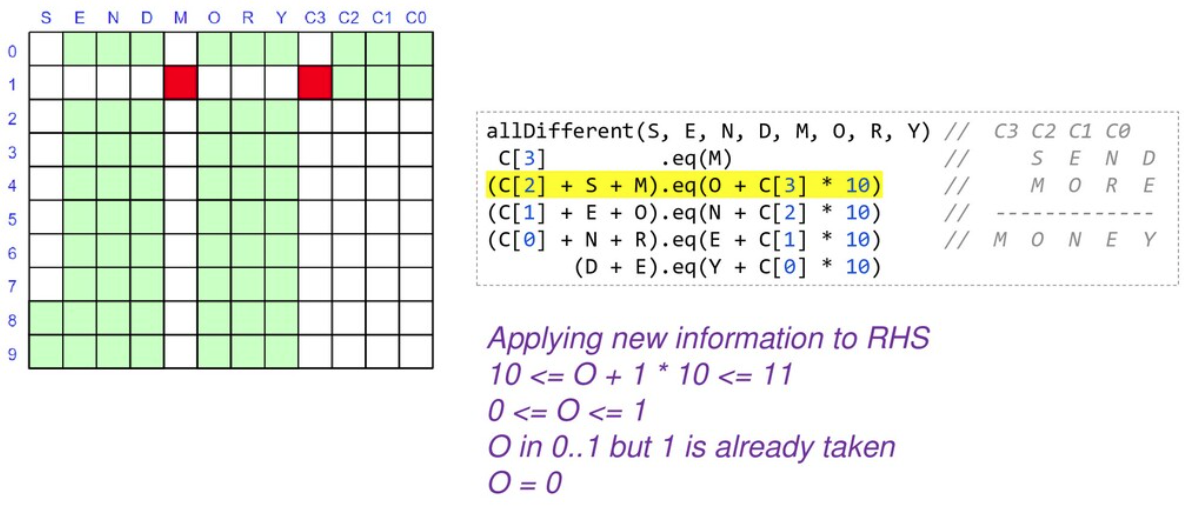
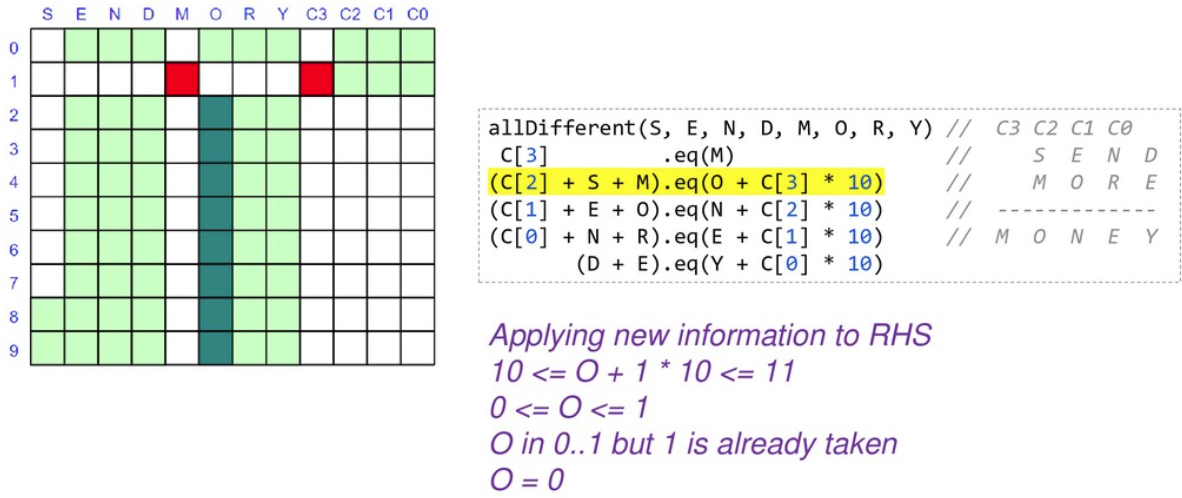
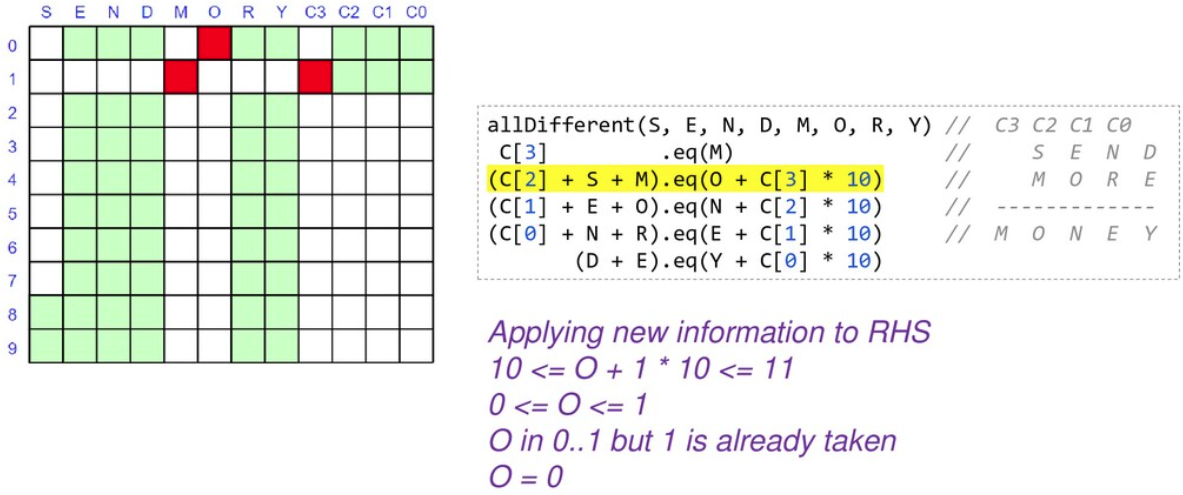

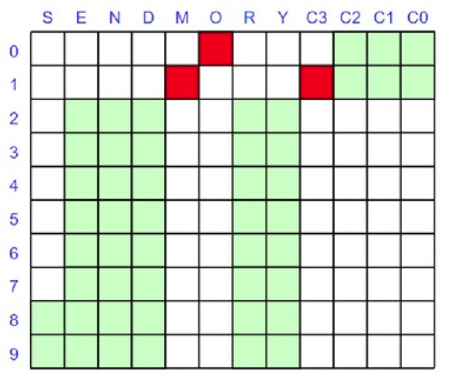
As we are locking in the value of variables, we can substitute them into and simplify our constraints. When we reapply them, they will be quicker to evaluate and may reveal more information.
At this point we only have 2 of our variables locked down but our search space is nearly half what we started with, and we have simplified some of our constraints. We would continue branching and solving at this point until we find our solution or determine that no solution is possible.
Looking at other languages
The example repo also contains solutions for this problem in other languages, so you can compare and contrast, including Clojure, Haskell (Frege), Java, JavaScript (Nashorn), Ruby (JRuby), Python (Jython), Kotlin, Lua (Luaj), Prolog (tuprolog), and Scala.

To wrap up, let’s look at solving a few more examples (using Choco). We’ll solve some of the examples from an interesting blog on the history of Cryptarithmetic problems:
-
ABCD * 4 = DCBA -
AA + BB + CC = ABC -
HALF + HALF = WHOLE -
HALF + FIFTH + TENTH + TENTH + TENTH = WHOLE
Here is the code:
new Model("ABCD*4=DCBA").with {
def (A, D) = ['A', 'D'].collect { intVar(it, 1, 9) }
def (B, C) = ['B', 'C'].collect { intVar(it, 0, 9) }
def R = (0..2).collect { intVar(0, 9) }
allDifferent(A, B, C, D).post()
R[2].add(A.mul(4)).eq(D).post()
R[1].add(B.mul(4)).eq(C.add(R[2].mul(10))).post()
R[0].add(C.mul(4)).eq(B.add(R[1].mul(10))).post()
D.mul(4).eq(A.add(R[0].mul(10))).post()
solver.findAllSolutions().each {
println "$name: ${pretty(it, [A, B, C, D, ' * 4 = ', D, C, B, A])}\n$it\n"
}
}
new Model("AA+BB+CC=ABC").with {
def (A, B, C) = ['A', 'B', 'C'].collect { intVar(it, 1, 9) }
allDifferent(A, B, C).post()
A.mul(11).add(B.mul(11).add(C.mul(11))).eq(A.mul(100).add(B.mul(10)).add(C)).post()
solver.findAllSolutions().each {
println "$name: ${pretty(it, [A, A, ' + ', B, B, ' + ', C, C, ' = ', A, B, C])}\n$it\n"
}
}
new Model("HALF+HALF=WHOLE").with {
def (H, W) = ['H', 'W'].collect { intVar(it, 1, 9) }
def (A, E, F, L, O) = ['A', 'E', 'F', 'L', 'O'].collect { intVar(it, 0, 9) }
allDifferent(H, W, A, E, F, L, O).post()
IntVar[] ALL = [
H, A, L, F,
W, H, O, L, E]
int[] COEFFS = [
2000, 200, 20, 2,
-10000, -1000, -100, -10, -1]
scalar(ALL, COEFFS, "=", 0).post()
solver.findAllSolutions().each {
println "$name: ${pretty(it, [H, A, L, F, ' + ', H, A, L, F, ' = ', W, H, O, L, E])}\n$it\n"
}
}
new Model("HALF+FIFTH+TENTH+TENTH+TENTH=WHOLE").with {
def (H, F, T, W) = ['H', 'F', 'T', 'W'].collect { intVar(it, 1, 9) }
def (A, L, I, E, N, O) = ['A', 'L', 'I', 'E', 'N', 'O'].collect { intVar(it, 0, 9) }
allDifferent(H, F, T, W, A, L, I, E, N, O).post()
IntVar[] ALL = [
H, A, L, F,
F, I, F, T, H,
T, E, N, T, H,
T, E, N, T, H,
T, E, N, T, H,
W, H, O, L, E]
int[] COEFFS = [
1000, 100, 10, 1,
10000, 1000, 100, 10, 1,
10000, 1000, 100, 10, 1,
10000, 1000, 100, 10, 1,
10000, 1000, 100, 10, 1,
-10000, -1000, -100, -10, -1]
scalar(ALL, COEFFS, "=", 0).post()
solver.findAllSolutions().each {
def parts = [H, A, L, F, '+', F, I, F, T, H, '+', T, E, N, T, H, '+',
T, E, N, T, H, '+', T, E, N, T, H, '=', W, H, O, L, E]
println "$name: ${pretty(it, parts)}\n$it\n"
}
}
// helper method to print solutions
def pretty(model, parts) {
parts.collect { p -> p instanceof IntVar ? model.getIntVal(p) : p }.join()
}which has this output:
ABCD*4=DCBA: 2178 * 4 = 8712 Solution: A=2, D=8, B=1, C=7, IV_1=3, IV_2=3, IV_3=0, (A*4)=8, sum_exp_4=8, (B*4)=4, …, AA+BB+CC=ABC: 11 + 99 + 88 = 198 Solution: A=1, B=9, C=8, (A*11)=11, (B*11)=99, (C*11)=88, …, HALF+HALF=WHOLE: 9604 + 9604 = 19208 Solution: H=9, W=1, A=6, E=8, F=4, L=0, O=2, HALF+HALF=WHOLE: 9703 + 9703 = 19406 Solution: H=9, W=1, A=7, E=6, F=3, L=0, O=4, HALF+HALF=WHOLE: 9802 + 9802 = 19604 Solution: H=9, W=1, A=8, E=4, F=2, L=0, O=6, HALF+FIFTH+TENTH+TENTH+TENTH=WHOLE: 6701+14126+25326+25326+25326=96805 Solution: H=6, F=1, T=2, W=9, A=7, L=0, I=4, E=5, N=3, O=8,
You should see the common patterns used for solving these puzzles.
Further Information
-
JaCoP Java Constraint Programming solver
-
Choco open source library for constraint programming
-
OR-Tools constraint optimization
-
Verbal arithmetic problems described (wikipedia)
-
JSR331 Constraint Programming API
-
Github repo containing sample code
Conclusion
We have looked at using Groovy and a few constraint programming libraries to solve a cryptarithmetic puzzles. Why not try solving some of your own puzzles.
